Täynnä dataa olevassa maailmassa uskomuksemme ja päätöksemme perustuvat yhä enemmän numeroiden ja tilastollisen analyysin pohjalle. Erityisesti näin markkinoinnin alalla, jossa tuijotamme päivät pitkät ruudulla olevia lukuja. Matka datasta johtopäätöksiin on kuitenkin usein hankalampi kuin osataan ennakoida. Esittelen neljä tilastollista harhapäätelmää, tai sudenkuoppaa, jotka voivat pahimmillaan johtaa täysin vääriin johtopäätöksiin.
- Perustasoharha
- Keskiarvojen harhaanjohtavuus
- Simpsonin paradoksi
- Epälineaariset suhteet
Perustasoharha: uhkien tunnistaminen lentokentällä
Perustasoharhaa voidaan havainnollistaa elävästi lentokenttäturvallisuuden kontekstissa. Kuvitellaan seulontatekniikka, joka on suunniteltu tunnistamaan mahdolliset uhat matkustajien joukosta 99 % tarkkuudella. Äkkiseltään tämä vaikuttaa erittäin tehokkaalta, mutta on kuitenkin ratkaisevan tärkeää tarkastella todellisten turvallisuusuhkien perustasoa.
- Esimerkki: Oletetaan, että miljoonan lentomatkustajan joukossa on yksi mahdollinen uhka. Seulontamenetelmä tunnistaa uhan oikein 99 % ajasta, mutta samaan aikaan se tunnistaa myös virheellisesti 1 % viattomista matkustajista uhkiksi.
- Tulos: Vaikka uhka melkein aina saadaankin kiinni, 1 %:n virheellisen positiivisen tuloksen vuoksi 9 999 viatonta matkustajaa merkitään myös potentiaalisiksi uhiksi.
- Seuraus: Huolimatta korkeasta tarkkuusasteesta, valtaosa hälytyksistä (yli 99,99 %) on virheellisiä positiivisia johtuen todellisten uhkien äärimmäisen alhaisesta perustasosta.
Perustason huomioon ottaminen on kriittistä kun arvioidaan turvallisuusjärjestelyjen tehokkuutta. Perustason huomiotta jättäminen johtaa järjestelmän käytännöllisen hyödyn yliarviointiin, eikä huomioi miten paljon haittaa järjestelmästä voi johtua lentokentän asiakkailla.
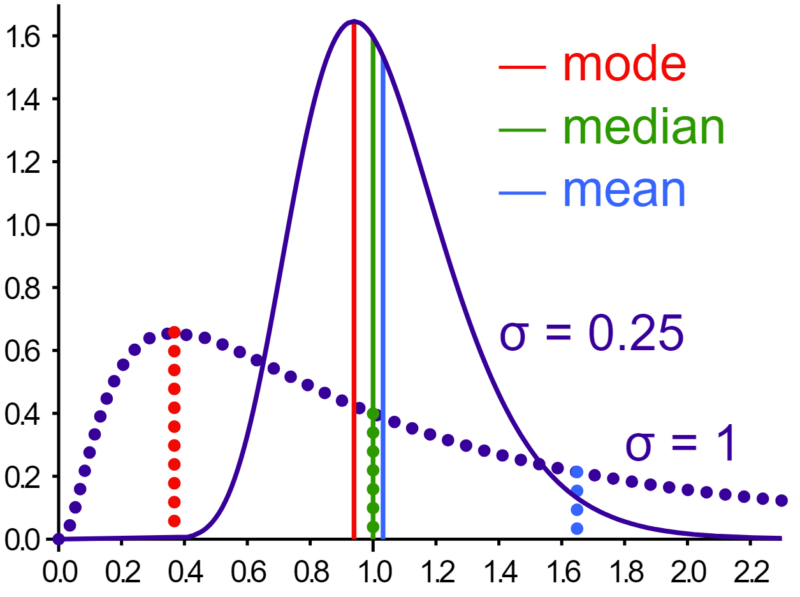
Keskiarvojen harhaanjohtava luonne oikealle vinoutuneissa jakaumissa: Varallisuuden jakautuminen
Oikealle vinoutunut jakauma on hyvä esimerkki siitä miten keskiarvoihin luottaminen voi harhauttaa tulkitsemaan dataa virheellisesti. Hyvä esimerkki tästä on kuvitteellinen maa, jossa suurin osa väestöstä omistaa suhteellisen vaatimattoman varallisuuden, kun taas hyvin pieni osuus omistaa merkittävän osan koko maan varallisuudesta.
- Esimerkki: Koko maan kaikkien asukkaiden varallisuuden keskiarvo on 300 000 euroa, mikä viittaisi suhteellisen mukavaan elintasoon kaikkialla.
- Tarkempi analyysi: 99% väestöstä omistaa keskimäärin 50 000 euron varallisuuden ja 1% väestöstä omistaa miljoonien varallisuuden. Äärimmäisen rikkaan yhden prosentin varallisuus nostaa keskiarvoa liian korkeaksi, jotta sillä voitaisiin luotettavasti arvioida keskimääräisen kansalaisen varallisuutta.
- Vaihtoehtoiset mittarit: Lähemmäksi 50 000 euroa osuva mediaani tarjoaisi tarkemman kuvan maan todellisesta tavan tallaajan varallisuudesta.
Varallisuuden jakautuminen on hyvä esimerkki siitä, miksi keskiarvoon ei aina ole luottamista hyvänä mittarina. Sen takia datan kokonaisjakaumaa on hyvä tarkastella laajemmin, jotta ymmärretään paremmin kokonaiskuva. Lisäksi on hyvä muistaa tarkastella myös esimerkiksi mediaania kun arvioit datasi keskimääräisiä arvoja.
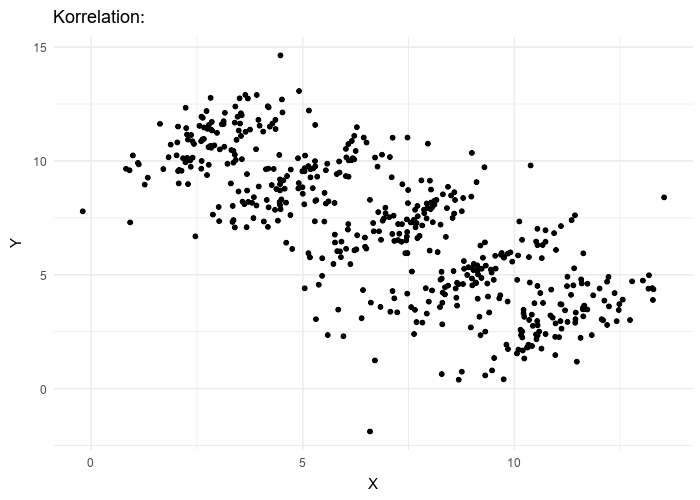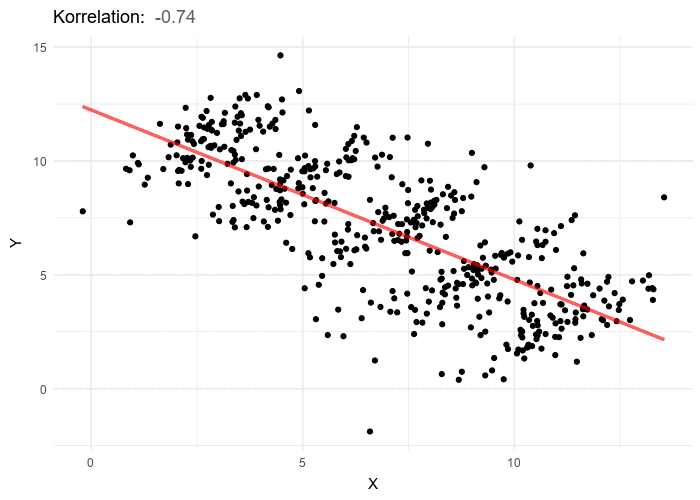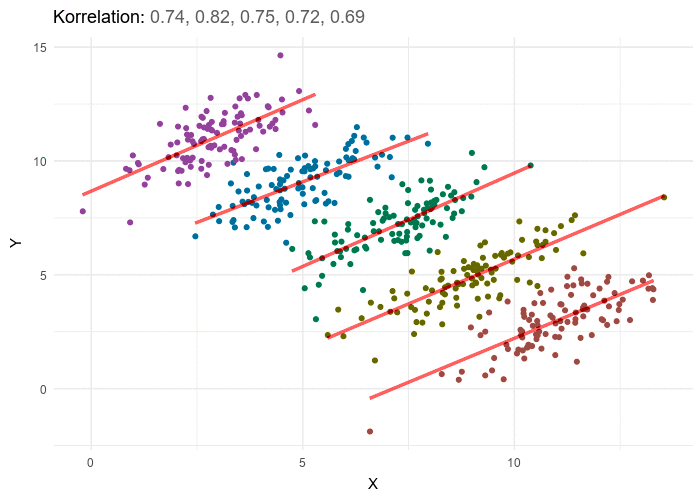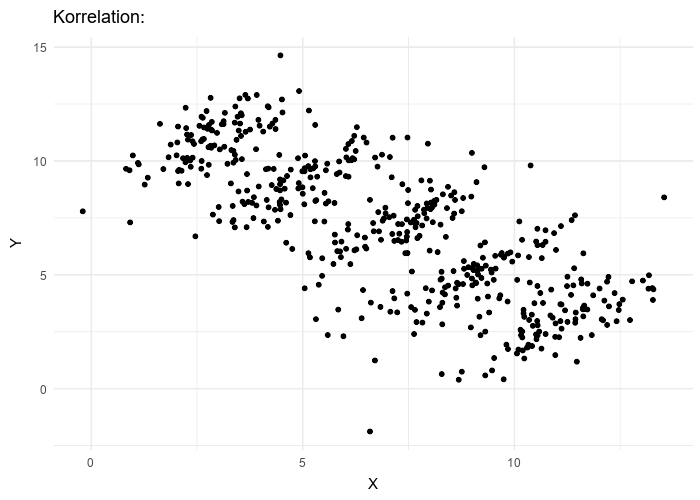
Simpsonin paradoksi: Sivumäärän vaikutus kirjamyyntiin
Kuvitellaan kustantamon datasetti, joka näyttää kokonaismyyntilukujen laskevan, kun kirjojen sivumäärä kasvaa. Ensivilkaisulla tämä viittaa siihen, että lukijat suosivat lyhyempiä kirjoja.
- Alkuperäinen analyysi: Yli 300 sivua sisältävät kirjat myyvät 20 % vähemmän kuin alle 300 sivun kirjat. Laskemme korrelaation ja saamme tilastollisesti merkittävän tuloksen, joka vahvistaa sivujen määrän lisääntymisen laskevan kirjojen myyntiä.
Tämä johtopäätös muuttuu kuitenkin, kun analysoimme dataa erottamalla sen kahteen kategoriaan: kovakantisiin ja pehmeäkantisiin kirjoihin.
- Kovakantiset kirjat: Kirjat joissa on yli 300 sivua, myyvät 30 % enemmän kuin niiden lyhyemmät vastineet.
- Pehmeäkantiset kirjat: Sama kaava,jossa pidemmät kirjat myyvät 25% enemmän kuin lyhyet kirjat.
Eron syynä on Simpsonin paradoksi
Simpsonin paradoksi on lyhyesti se, että trendi joka näkyy kokonaiskuvassa voi kääntyä päälaelleen kun data segmentoidaan ryhmiin.
Tässä tapauksessa paradoksi syntyy, koska yleensä pidemmät kovakantiset kirjat houkuttelevat pienempää, mutta omistautuneempaa markkinaa. Pehmeäkantiset kirjat puolestaan palvelevat laajempaa markkinaa, joka ostaa kirjoja laajemmalta sivumääräalueelta. Yhdistettynä pehmeäkantisten kirjojen ylivoimainen myyntimäärä laimentaa kovakantisten kirjojen näkyvää vaikutusta, peittäen todellisen trendin kussakin kategoriassa. Aggregoitu data voi johtaa vääriin johtopäätöksiin, joka korostaa segmentoidun datan tärkeyttä todellisten trendien ymmärtämisessä.
Epälineaariset suhteet: Online-mainonnan kulutus
Esimerkkinä epälineaaristen suhteiden monimutkaisuudesta otetaan verkkokaupan online mainonnan kulutus ja sen vaikutus myyntiin. Tältä voisi odottaa lineaarista suhdetta: kun mainonnan kulutus kasvaa, myös myynti kasvaa. Todellisuus on kuitenkin monimutkaisempi.
- Alkuperäinen investointi: Pienet lisäykset mainonnan kulutuksessa johtavat merkittäviin hyppyihin myynnissä, viitaten lähes eksponentiaalista kasvua. Tämä johtuu siitä, että alkuperäinen mainonta tavoittaa suuren, hyödyntämättömän yleisön.
- Tuottojen väheneminen: Tietyn pisteen jälkeen lisämainonnan kulutus tuottaa pienempiä lisäyksiä myyntii. Markkina tulee kyllästetyksi, ja useimmat potentiaaliset asiakkaat ovat jo tietoisia tuotteesta. Samalla määrällä euroja ei saa enää yhtä paljon myyntiä.
- Odottamaton nousu: Odottamaton käänne tapahtuu, kun suuri näkyvyys mainonnan kautta johtaa puskaradiosuosituksiin. Tämä “ilmainen” mainonta lisää myyntiä ilman lisäkuluja. Tämä voi luoda tilanteen, jossa myynnin kasvu alkaa kiihtyä uudelleen tietyn mainonnan kulutustason jälkeen.
Konkreettinen esimerkki:
- Yritys käyttää 10 000 euroa digimainoksiin ja saa myyntiä 5000 kappaletta.
- Rohkaistuneena he lisäävät kulutustaan 20 000 euroon, odottaen lineaarista kasvua. Kuitenkin myynti kasvaa vain 8000 kappaleeseen, eikä odotettuun 10 000 kappaleeseen.
- Jatkaessaan kulutuksen lisäämistä, tuoton kasvuvauhti vähenee, kunnes he käyttävät 50 000 euroa ja puskaradio alkaa lisätä myyntiä. Lopulta myynti tasaantuu 35 000 kappaleeseen. Lineaarisella mallilla laskettuna 50 000 eurolla pitäisi saada myytyä 25 000 kappaletta.
Ole tarkkana analyyseissäsi
Kun analysoit markkinoinnin, tai mitä vain dataa, muista aina pysähtyä miettimään mitä teet. Monesti liian nopeat johtopäätökset voivat johtaa harhaan ja pahimmillaan teet niiden perusteella vääriä päätöksiä. Yritä aina ymmärtää datasi luonne ennen kuin teet hätiköityjä päätöksiä ensimmäisten analyysiesi perusteella.
Muista tarkistaa seuraavat asiat, kun seuraavan kerran lähdet tekemään anlyysia:
- Suhdelukuja laskiessa ja vertaillessa muista tarkistaa käyttämiesi datajoukkojen perustaso. Tarkista vertailetko keskenään kahta hyvin erikokoista tai erilaista joukkoa. Onko kahdessa vertailtavassa joukossa perustavanlaatuisia eroja, jotka vaikuttavat analyysisi tulkintaan?
- Keskiarvoja laskiessa ja yleistyksiä tehdessä muista tarkastella dataa myös kokonaisuutena. Joskus keskiarvot antavat vääristyneen kuvan datan jakaumasta.
- Trendejä analysoitaessa muista pilkkoa data osiin ennen kuin teet lopulliset johtopäätökset. Kokonaisdatan trendit voivat olla harhaanjohtavia, kun sitä ei ole segmentoitu.
- Ennustaessa tulevaa muista, että oikea maailma ei aina liiku lineaarisesti eteenpäin. +10 X ei aina tarkoita suoraan +10 Y.
